matematicas discretas
sábado, 9 de diciembre de 2023
arboles y grafos
ARBOLES Y GRAFOS
En este contexto árboles y grafos se refiere a estructuras de datos que permiten organizar y mantener información en un computador. Esta forma se inspira una forma de organizar información con lápiz y papel usando nodos y flechas entre los nodos (a esas flechas también se les llama arcos, a los nodos también se les llama vértices). Los grafos y árboles en papel son apropiados por ejemplo para capturar sólo una parte de la información de objetos, situaciones y otros tipos de información (i.e son apropiados para abstraer).
En un computador además de permitir organizar información, resultan estructuras útiles para resolver ciertos tipos de problema (por ejemplo pueden emplearse árboles AVL para mantener información ordenada de forma eficiente).
Para jugar, entender y emplear mejor grafos (y árboles) varias personas (e.g Euler) han propuesto definiciones; a partir de estas definiciones y con ayuda de razonamientos lógicos han demostrado propiedades. Un mínimo de definiciones y de propiedades de grafos y árboles se presenta a continuación.
Note que para ver mejor esta página puede requerir configurar su navegador para que presente símbolos especiales, que se esperan con el tipo de letra de symbol. En el caso del navegador Mozilla, y suponiendo que en su sistema ya está instalado y configurado para Mozilla el tipo de letra para símbolos marque el botón de chequeo que permite que el documento use otras fuentes, en el menú apariencia del diálogo de preferencias (elemento del menú editar).
Árbol
En ciencias de la informática, un árbol es una estructura de datos ampliamente usada que imita la forma de un árbol (un conjunto de nodos conectados). Un nodo es la unidad sobre la que se construye el árbol y puede tener cero o más nodos hijos conectados a él. Se dice que un nodo a es padre de un nodo b si existe un enlace desde a hasta b (en ese caso, también decimos que b es hijo de a). Sólo puede haber un único nodo sin padres, que llamaremos raíz. Un nodo que no tiene hijos se conoce como hoja. Los demás nodos (tienen padre y uno o varios hijos) se les conoce como rama.
Un árbol se define
como un tipo de grafo que no contiene ciclos, es decir es un grafo también
acíclico, pero a su vez es conexo. Tal es el caso de los siguientes dos grafos
en donde se puede notar que ninguno de los dos contiene repeticiones (ciclos).
Bosques de árboles.
Los bosques de árboles son un caso similar a los árboles, son acíclicos, pero
no son conexos. Como ejemplo tenemos la siguiente figura.
Formalmente, podemos definir un árbol de la siguiente forma:
Caso base: un árbol con sólo un nodo (es a la vez raíz del árbol y hoja).
Un nuevo árbol a partir de un nodo nr y k árboles de raíces con elementos cada
uno, puede construirse estableciendo una relación padre-hijo entre nr y cada
una de las raíces de los k árboles. El árbol resultante de nodos tiene como
raíz el nodo nr, los nodos son los hijos de nr y el conjunto de nodos hoja está
formado por la unión de los k conjuntos hojas iniciales. A cada uno de los
árboles Ai se les denota ahora subárboles de la raíz.
Una sucesión de nodos del árbol, de forma que entre cada dos nodos consecutivos
de la sucesión haya una relación de parentesco, decimos que es un recorrido
árbol. Existen dos recorridos típicos para listar los nodos de un árbol:
primero en profundidad y primero en anchura. En el primer caso, se listan los
nodos expandiendo el hijo actual de cada nodo hasta llegar a una hoja, donde se
vuelve al nodo anterior probando por el siguiente hijo y así sucesivamente. En
el segundo, por su parte, antes de listar los nodos de nivel n + 1 (a distancia
n + 1 aristas de la raíz), se deben haber listado todos los de nivel n. Otros
recorridos típicos del árbol son preorden, postorden e inorden:
El recorrido en preorden, también llamado orden previo consiste en recorrer en
primer lugar la raíz y luego cada uno de los hijos en orden previo.
El recorrido en inorden, también llamado orden simétrico (aunque este nombre
sólo cobra significado en los árboles binarios) consiste en recorrer en primer
lugar A1, luego la raíz y luego cada uno de los hijos en orden simétrico.
El recorrido en postorden, también llamado orden posterior consiste en recorrer
en primer lugar cada uno de los hijos en orden posterior y por último la raíz.
Finalmente, puede decirse que esta estructura es una representación del
concepto de árbol en teoría de grafos. Un árbol es un grafo conexo y acíclico
(ver también teoría de grafos y Glosario en teoría de grafos).
Tipos de árboles
-Árbol binario
En ciencias de la computación, un árbol binario es una estructura de datos en
la cual cada nodo siempre tiene un hijo izquierdo y un hijo derecho. No pueden
tener más de dos hijos (de ahí el nombre "binario"). Si algún hijo
tiene como referencia a null, es decir que no almacena ningún dato, entonces
este es llamado un nodo externo. En el caso contrario el hijo es llamado un
nodo interno. Usos comunes de los árboles binarios son los árboles binarios de
búsqueda, los montículos binarios y Codificación de Huffman.
Tipos de árboles binarios
Un árbol binario es un árbol con raíz en el que cada nodo tiene como
máximo dos hijos.
Un árbol binario lleno es un árbol en el que cada nodo tiene cero o dos
hijos.
Un árbol binario perfecto es un árbol binario lleno en el que todas las
hojas (vértices con cero hijos) están a la misma profundidad (distancia desde
la raíz, también llamada altura).
A veces un árbol binario perfecto es denominado árbol binario completo. Otros
definen un árbol binario completo como un árbol binario lleno en el que todas
las hojas están a profundidad n o n-1, para alguna n.
Un árbol binario es un árbol en el que ningún nodo puede tener más de dos
subárboles. En un árbol binario cada nodo puede tener cero, uno o dos hijos
(subárboles). Se conoce el nodo de la izquierda como hijo izquierdo y el nodo
de la derecha como hijo derecho.
-Árbol binario de búsqueda auto-balanceable
En ciencias de la computación, un árbol binario de búsqueda auto-balanceable o
equilibrado es un árbol binario de búsqueda que intenta mantener su altura, o
el número de niveles de nodos bajo la raíz, tan pequeños como sea posible en
todo momento, automáticamente. Esto es importante, ya que muchas operaciones en
un árbol de búsqueda binaria tardan un tiempo proporcional a la altura del
árbol, y los árboles binarios de búsqueda ordinarios pueden tomar alturas muy
grandes en situaciones normales, como cuando las claves son insertadas en
orden. Mantener baja la altura se consigue habitualmente realizando
transformaciones en el árbol, como la rotación de árboles, en momentos clave.
Tiempos para varias operaciones en términos del número de nodos en el árbol n:
Operación Tiempo en cota superior asintótica
Búsqueda O(log n)
Inserción O(log n)
Eliminación O(log n)
Iteración en orden O(n)
Para algunas implementaciones estos tiempos son el peor caso, mientras que para
otras están amortizados.
Estructuras de datos populares que implementan este tipo de árbol:
Árbol AVL
Árbol rojo-negro
-Árbol-B
En las ciencias de la computación, los árboles-B ó B-árboles son estructuras de
datos de árbol que se encuentran comúnmente en las implementaciones de bases de
datos y sistemas de archivos. Los árboles B mantienen los datos ordenados y las
inserciones y eliminaciones se realizan en tiempo logarítmico amortizado.
B-árbol es un árbol de búsqueda que puede estar vacío o aquel cuyos nodos
pueden tener varios hijos, existiendo una relación de orden entre ellos, tal
como muestra el dibujo.
Un árbol-B de orden M (el máximo número de hijos que puede tener cada nodo) es
un árbol que satisface las siguientes propiedades:
1.Cada nodo tiene como máximo M hijos.
2.Cada nodo (excepto raíz y hojas) tiene como mínimo M/2 hijos.
3.La raíz tiene al menos 2 hijos si no es un nodo hoja.
4.Todos los nodos hoja aparecen al mismo nivel.
5.Un nodo no hoja con k hijos contiene k-1 elementos almacenados.
6.Los hijos que cuelgan de la raíz (r1, ···, rm) tienen que cumplir ciertas
condiciones:
1.El primero tiene valor menor que r1.
2.El segundo tiene valor mayor que r1 y menor que r2, etc.
3.El último hijo tiene valor mayor que rm.
-Árbol multicamino
Los árboles multicamino o árboles multirrama son estructuras de datos de tipo
árbol usadas en computación.
Un árbol multicamino posee un grado g mayor a dos, donde cada nodo de
información del árbol tiene un máximo de g hijos.
Sea un árbol de m-caminos A, es un árbol m-caminos si y solo si:
A está vacío
Cada nodo de A muestra la siguiente estructura:
[nClaves,Enlace0,Clave1,...,ClavenClaves,EnlacenClaves]
nClaves es el número de valores de clave de un nodo, pudiendo ser: 0 <=
nClaves <= g-1 Enlacei, son los enlaces a los subárboles de A, pudiendo ser:
0 <= i <= nClaves Clavei, son los valores de clave, pudiendo ser: 1 <=
i <= nClaves Clavei < g =" (V,A,j" g1 =" (V1," v1
=" {1," a1 =" {(1," g2 =" (V2," v2 ="
{1," a2 =" {(1," g3 =" (V3," v3 =" {1," a3
=" {">, <2,>, <2,> }
Gráficamente estas tres estructuras de vértices y arcos se pueden representar
de la siguiente manera:
Algunos de los principales tipos de grafos son los que se muestran a
continuación:
•Grafo regular: Aquel con el mismo grado en todos los vértices. Si ese grado es
k lo llamaremos k-regular.
•Grafo bipartito: Es aquel con cuyos vértices pueden formarse dos conjuntos
disjuntos de modo que no haya adyacencias entre vértices pertenecientes al
mismo conjunto
•Grafo completo: Aquel con una arista entre cada par de vértices. Un grafo
completo con n vértices se denota Kn.
•Un grafo bipartito regular: se denota Km,n donde m, n es el grado de cada
conjunto disjunto de vértices.
•Grafo nulo: Se dice que un grafo es nulo cuando los vértices que lo componen
no están conectados, esto es, que son vértices aislados.
•Grafos Isomorfos: Dos grafos son isomorfos cuando existe una correspondencia
biunívoca (uno a uno), entre sus vértices de tal forma que dos de estos quedan
unidos por una arista en común.
•Grafos Platónicos: Son los Grafos formados por los vértices y aristas de los
cinco sólidos regulares (Sólidos Platónicos), a saber, el tetraedro, el cubo,
el octaedro, el dodecaedro y el icosaedro.
Grafos Eulerianos.
Para definir un camino euleriano es importante definir un camino euleriano
primero. Un camino euleriano se define de la manera más sencilla como un camino
que contiene todos los arcos del grafo.
Teniendo esto definido podemos hablar de los grafos eulerianos describiéndolos
simplemente como aquel grafo que contiene un camino euleriano. Como ejemplos
tenemos las siguientes imágenes:
El primer grafo de ellos no contiene caminos eulerianos mientras el segundo
contiene al menos uno.
Grafos Conexos.
Un grafo se puede definir como conexo si cualquier vértice V pertenece al
conjunto de vértices y es alcanzable por algún otro. Otra definición que
dejaría esto más claro sería: "un grafo conexo es un grafo no dirigido de
modo que para cualquier par de nodos existe al menos un camino que los
une".
Recorrido de un grafo.
Recorrer un grafo significa tratar de alcanzar todos los nodos que estén
relacionados con uno que llamaremos nodo de salida. Existen básicamente dos
técnicas para recorrer un grafo: el recorrido en anchura; y el recorrido en
profundidad.
•Recorrido en anchura: El recorrido en anchura supone recorrer el grafo, a
partir de un nodo dado, en niveles, es decir, primero los que están a una
distancia de un arco del nodo de salida, después los que están a dos arcos de
distancia, y así sucesivamente hasta alcanzar todos los nodos a los que se
pudiese llegar desde el nodo salida.
•Recorrido en profundidad: el recorrido en profundidad trata de buscar los
caminos que parten desde el nodo de salida hasta que ya no es posible avanzar
más. Cuando ya no puede avanzarse más sobre el camino elegido, se vuelve atrás
en busca de caminos alternativos, que no se estudiaron previamente.
Representación de grafos en programas.
Hay tres maneras de representar un grafo en un programa: mediante matrices,
mediante listas y mediante matrices dispersas.
•Representación mediante matrices: La forma más fácil de guardar la
información de los nodos es mediante la utilización de un vector que indexe los
nodos, de manera que los arcos entre los nodos se pueden ver como relaciones
entre los índices. Esta relación entre índices se puede guardar en una matriz,
que llamaremos de adyacencia.
•Representación mediante listas: En las listas de adyacencia lo que
haremos será guardar por cada nodo, además de la información que pueda contener
el propio nodo, una lista dinámica con los nodos a los que se puede acceder
desde él. La información de los nodos se puede guardar en un vector, al igual
que antes, o en otra lista dinámica.
•Representación mediante matrices dispersas: Para evitar uno de los
problemas que teníamos con las listas de adyacencia, que era la dificultad de
obtener las relaciones inversas, podemos utilizar las matrices dispersas, que
contienen tanta información como las matrices de adyacencia, pero, en
principio, no ocupan tanta memoria como las matrices, ya que al igual que en
las listas de adyacencia, sólo representaremos aquellos enlaces que existen en
el grafo.
Dígrafo (grafo dirigido).
A un grafo dirigido
se le puede definir como un grafo que contiene aristas dirigidas, como en el
siguiente caso.
Aplicaciones de los dígrafos
Una de las aplicaciones mas importantes es de hallar el camino mas corto hacia
un destino, ya sea de una ciudad a otra, de unos departamentos a otros, para el
recorrido de árboles, sirve para la representación de algoritmos, etc. Un
ejemplo de esto es la tarea de freír un huevo.
Grado de un grafo.
•Grado de incidencia positivo: El grado de incidencia positivo de un
nodonjes el número de arcos que tienen como nodo inicial anj. Ejemplo: El grado
de incidencia de 1 es igual a 3.
•Grado de incidencia negativo: El grado de incidencia negativo de un
nodonjes el número de arcos que terminan ennj. Ejemplo: El grado de incidencia
negativo de 1 es igual a 1.
•Grado de un nodo: Paradigrafoses el grado de incidencia positivo menos el
grado de incidencia negativo del nodo. Ejemplo: El grado de 1 es igual a 3 –1 =
2, el grado del nodo 4 es 2 –2 = 0. Para grafos no dirigidos es el número de
líneas asociadas al nodo.
Ciclo de un grafo.
Ciclo: Es una cadena finita donde el nodo inicial de la cadena coincide
con el nodo terminal de la misma.
•Ciclo simple: Es el ciclo que a su vez es una cadena simple.
Estructuras no lineales: Grafos
Las estructuras de datos no lineales se caracterizan por no existir una
relación de adyacencia, entre sus elementos, es decir, un elemento puede estar
relacionado con cero, uno o más elementos.
La estructura no lineal de datos más general es el grafo donde sus nodos pueden
relacionarse de cualquier manera sin una relación de orden predefinida.
Estructuras no lineales: Grafos Entre las múltiples aplicaciones que tienen
estas estructuras podemos mencionar:•Para modelar diversas situaciones tales
como: sistemas de aeropuertos, flujo de tráfico, y responder a preguntas como:
¿Qué tiempo es más corto?, ¿Cómo es más barato?, o ¿Qué camino es más corto?.
•Los grafos también son utilizados para realizar planificación de actividades,
tareas del computador, planificar operaciones en lenguaje de máquinas para
minimizar tiempo de ejecución.¿Qué tarea debo hacer primero?. •Para representar
circuitos eléctricos, de aguas etc... , y preguntar, están todas las
componentes conectadas.
Grafos Los grafos pueden ser utilizados como la estructura básica para
múltiples aplicaciones en el área de la Computación. Un grafo G (N, A, f) es un
conjunto no vacío, donde:•N={n1, n2, ... ,nM) es el conjunto de nodos o
vértices•A={a1, a2, ..., a K} es el conjunto de aristas y•La función f : R
→ΜΧΜindica los pares de nodos que estαn relacionados.•Grafos Dirigidos
(Dígrafos) En estos grafos, las aristas que comunican dos nodos tienen un único
sentido, una arista puede ir de x a y, pero no de y a x. Se expresa
gráficamente con flechas que indican el sentido de la relación entre cada par
de nodos.
Grafos•Grafos no dirigidos En estos grafos, las aristas que comunican dos nodos
tienen dos sentidos. Si una arista va de x a y, la misma arista va de y a x. Se
expresa gráficamente por líneas. La representación gráfica de un grafo se
define con un círculo o rectángulo para los nodos y las relaciones con líneas o
flechas según sea un grafo no dirigido o un dígrafo, respectivamente.
lunes, 27 de noviembre de 2023
representacion de grafos
REPRESENTACIÓN DE LOS GRAFOS.
- Representación por incidencia.
- Lista de incidencia: El grafo está representado por un arreglo de aristas, identificadas por un de pares de vértices, que son los que conecta esa arista.
- Matriz de incidencia: El grafo está representado por una matriz de A (aristas) por V (vértices), donde [arista, vértice] contiene la información de la arista (conectado o no conectado).
- Representación por adyacencia.
- Listas de adyacencia: El grafo está representado por un arreglo de listas de adyacencia. Para un vértice i, la lista de adyacencia está formada por todos los vértices adyacentes a i. Puede construirse en tiempo lineal, y las inserciones pueden hacerse al principio de cada lista, con lo que se asegura tiempo constante.
- Matriz de adyacencia: Una matriz de adyacencia es una matriz M de dimensión n*n, en donde n es el número de vértices que almacena valores booleanos, donde M[i,j] es verdadero (o contiene un peso) si y solo si existe un arco que vaya del vértice i al vértice j. La inicialización llevaría un tiempo del O ( #(V2)).
- Estructura de lista:
- Lista de incidencia: Las aristas son representadas con un vector de pares (ordenados, si el grafo es dirigido), donde cada par representa una de las aristas.
- Lista de adyacencia: Cada vértice tiene una lista de vértices los cuales son adyacentes a él. Esto causa redundancia en un grafo no dirigido (ya que A existe en la lista de adyacencia de B y viceversa), pero las búsquedas son más rápidas, al costo de almacenamiento extra.
- Lista de grados: También llamada secuencia de grados o sucesión gráfica de un grafo no-dirigido es una secuencia de números, que corresponde a los grados de los vértices del grafo.
- Estructuras matriciales:
- Matriz de adyacencia: El grafo está representado por una matriz cuadrada M de tamaño, donde es el número de vértices. Si hay una arista entre un vértice x y un vértice y, entonces el elemento es 1, de lo contrario, es 0.
- Matriz de incidencia: El grafo está representado por una matriz de A (aristas) por V (vértices), donde [arista, vértice] contiene la información de la arista (1 - conectado, 0 - no conectado).
grafos
ELEMENTOS, CARACTERÍSTICAS Y COMPONENTES DE LOS GRAFOS.
ELEMENTOS Y CARACTERÍSTICAS.
COMPONENTES.
- Aristas.
- Aristas Adyacentes: Se dice que dos aristas son adyacentes si convergen en el mismo vértice.
- Aristas Paralelas: Se dice que dos aristas son paralelas si vértice inicial y el final son el mismo.
- Aristas Cíclicas: Arista que parte de un vértice para entrar en el mismo.
- Cruce: Son dos aristas que cruzan en un punto.
- Vértices.
- Vértices Adyacentes: Si tenemos un par de vértices de un grafo (U, V) y si tenemos un arista que los une, entonces U y V son vértices adyacentes y se dice que U es el vértice inicial y V el vértice adyacente.
- Vértice Aislado: Es un vértice de grado cero.
- Vértice Terminal: Es un vértice de grado 1.
5.1.1 TIPOS DE GRAFOS.
- Grafo simple: Se dice que el grafo G = (V, E) es un grafo simple de grado n si todos sus vértices tienen grado n.
- Grafo completo: Un grafo es completo si cada par de vértices está unido por una arista. Se denota por Kn al grafo completo de n vértices.
- Grafo bipartido: Un grafo es bipartido si V=V1?V2 y cada arista de E une un vértice de V1 y otro de V2.
- Grafo bipartido completo: Un grafo es bipartido completo si V=V1?V2 y dos vértices de V están unidos por una arista de E si y solo si un vértice está en V1 y el otro en V2. Se denota por Kr, donde V1 tiene r vértices y V2 tiene s vértices.
- Grafos planos: Un grafo plano es aquel que puede ser dibujado en el plano sin que ninguna arista se intersecta.
- Grafos conexos: Un grafo es conexo si cada par de vértices está conectado por un camino; es decir, si para cualquier par de vértices (a, b), existe al menos un camino posible desde "a" hacia "b".
- Grafo ponderado: Un grafo es ponderado si presenta los pesos de cada arista y se puede determinar la longitud de una ruta, la cual es la suma de todos los pesos de las aristas.
miércoles, 18 de octubre de 2023
algebra boleana
Álgebra booleana
¿Qué es el álgebra booleana?
El álgebra booleana, o álgebra de Boole, es una estructura algebraica que esquematiza las operaciones lógicas. Se usa para el tratamiento de variables binarias. Cubre los estudios de toda variable que solo tenga 2 resultados posibles, complementarios y excluyentes entre sí.
Por ejemplo, las variables cuya única posibilidad es verdadero o falso, correcto o incorrecto, encendido o apagado, son la base del estudio del álgebra booleana.
El álgebra booleana constituye la base de la electrónica digital y la informática. Se rige por el concepto de las compuertas lógicas, donde las operaciones conocidas en el álgebra tradicional se ven notablemente afectadas.
Historia del álgebra booleana
El matemático inglés George Boole (1816-1864), autodidacta, fue el primero en definir esta operación algebraica como parte de un sistema lógico, en 1854. Su inquietud surgió de una disputa existente entre Augustus De Morgan y William Hamilton, sobre los parámetros que definen este sistema lógico.
George Boole argumentó que la definición de los valores numéricos 0 y 1 corresponde, en el campo de la lógica, a la interpretación Nada y Universo, respectivamente.
La intención de Boole fue definir, a través de las propiedades del álgebra, las expresiones de la lógica proposicional necesarias para tratar con variables de tipo binario.
En 1854 se publicaron los apartados más significativos del álgebra booleana en el libro Una investigación de las leyes del pensamiento sobre las que se fundamentan las teorías matemáticas de la lógica y probabilidad.
Este curioso título sería resumido más adelante como The laws of thought (Las leyes del pensamiento). El título saltó a la fama debido a la inmediata atención que tuvo por parte de la comunidad matemática del momento.
En 1948, Claude Shannon la aplicó en el diseño de circuitos de conmutación eléctrica biestables. Esto sirvió como introducción a la aplicación del álgebra booleana en todo el esquema electrónico-digital,
Estructura del álgebra booleana
Los valores elementales en este tipo de álgebra son 0 y 1, que corresponden a FALSO y VERDADERO, respectivamente. Las operaciones fundamentales en el álgebra booleana son 3:
- Operación AND o conjunción. Representada por un punto ( . ). Sinónimo del producto.
- Operación OR o disyunción. Representada por una cruz ( + ) .Sinónimo de la suma.
- Operación NOT o negación. Representada por el prefijo NOT (NOT A). También se conoce como complemento.
Si en un conjunto A se definen 2 leyes de composición interna denotadas como producto y suma ( . + ), se dice que la terna ( A . + ) es un álgebra booleana si y solo si dicha terna cumple con la condición de ser un retículo distributivo.
Para definir un retículo distributivo se deben cumplir las condiciones de distribución entre las operaciones dadas:
. es distributiva con respecto a la suma + a . ( b + c ) = ( a . b ) + ( a . c )
+ es distributiva con respecto al producto. a + ( b . c ) = ( a + b ) . ( a + c )
Los elementos que componen el conjunto A deben ser binarios, teniendo así valores de universo o vacío.
Aplicaciones del álgebra booleana
Su mayor escenario de aplicación es la rama digital, donde sirve para estructurar los circuitos que componen las operaciones lógicas involucradas. El arte de la simplicidad de circuitos en pro de optimizar los procesos, es el resultado de la correcta aplicación y práctica del álgebra booleana.
Desde la elaboración de tableros eléctricos, pasando por la transmisión de datos, hasta llegar a la programación en diferentes lenguajes, podemos encontrar frecuentemente el álgebra de Boole en todo tipo de aplicaciones digitales.
Las variables booleanas son muy comunes en la estructura de la programación. Dependiendo del lenguaje de programación utilizado, existirán operaciones estructurales del código que usen dichas variables. Los condicionales y argumentos de cada lenguaje admiten variables booleanas para definir los procesos.
Postulados del álgebra booleana
Existen teoremas que rigen las leyes lógicas estructurales del álgebra booleana. De igual forma, se tienen postulados para conocer los resultados posibles en diferentes combinaciones de variables binarias, según la operación que se realice.
Suma (+)
El operador OR, cuyo elemento lógico es la unión (U), queda definido para variables binarias de la siguiente manera:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 1
Producto (.)
El operador AND, cuyo elemento lógico es la intersección (∩), queda definido para variables binarias de la siguiente manera:
0 . 0 = 0
0 . 1 = 0
1 . 0 = 0
1 . 1 = 1
Opuesto (NOT)
El operador NOT, cuyo elemento lógico es el complemento (X)’, queda definido para variables binarias de la siguiente manera:
NOT 0 = 1
NOT 1 = 0
Muchos de los postulados difieren de sus equivalentes en el álgebra convencional. Esto es debido al dominio de las variables. Por ejemplo, la adición de elementos universo en álgebra booleana (1 + 1) no puede arrojar el resultado convencional de 2, debido a que no pertenece a los elementos del conjunto binario.
Teoremas del álgebra booleana
Regla del cero y la unidad
Toda operación simple que involucre un elemento con las variables binarias, queda definida:
0 + A = A
1 + A = 1
0 . A = 0
1 . A = A
Potencias iguales o idempotencia
Las operaciones entre variables iguales quedan definidas como:
A + A = A
A . A = A
Complementación
Toda operación entre una variable y su complemento queda definida como:
A + NOT A = 1
A . NOT A = 0
Involución o doble negación
Toda doble negación sera considerada como la variable natural.
NOT (NOT A ) = A
Conmutativa
A + B = B + A : Conmutatividad de la suma.
A . B = B . A : Conmutatividad del producto.
Asociativa
A + ( B + C ) = ( A + B ) + C = A + B + C : Asociatividad de la suma.
A . ( B . C ) = ( A . B ) . C = A . B . C : Asociatividad del producto.
Distributiva
A + ( B . C ) = ( A + B ) . ( A + C ) : Distributividad de la suma con respecto al producto.
A . ( B + C ) = ( A . B ) + ( A + C ) : Distributividad del producto con respecto a la suma.
Leyes de absorción
Existen muchas leyes de absorción entre múltiples referencias, algunas de las más conocidas son:
A . ( A + B ) = A
A . ( NOT A + B ) = A . B
NOT A ( A + B ) = NOT A . B
( A + B ) . ( A + NOT B ) = A
A + A . B = A
A + NOT A . B = A + B
NOT A + A . B = NOT A + B
A . B + A . NOT B = A
Teorema de Morgan
Son leyes de transformación, que manejan pares de variables que interactúan entre las operaciones definidas del álgebra booleana ( + . ).
NOT ( A . B ) = NOT A + NOT B
NOT ( A +B ) = NOT A . NOT B
A + B = NOT ( NOT A + NOT B )
A . B = NOT ( NOT A . NOT B )
Dualidad
Todos los postulados y teoremas poseen la facultad de la dualidad. Esto implica que al intercambiar las variables y operaciones se verifica la proposición resultante. Es decir, que al intercambiar 0 por 1 y AND por OR o viceversa, se crea una expresión que también será completamente válida.
Por ejemplo, si se toma el postulado
1 . 0 = 0
Y se le aplica la dualidad
0 + 1 = 1
Se obtiene otro postulado perfectamente válido.
martes, 3 de octubre de 2023
lunes, 25 de septiembre de 2023
relacion de equivalencia y orden
Equivalencia | orden |
Una relación es una correspondencia entre un conjunto y si mismo, es decir entre A y A. | La relación queda formada por el subconjunto de pares que podemos formar con los elementos de A
|
Cuando se cumplen las propiedades: § Reflexiva. § Simétrica. § Transitiva.
| Si se cumplen: § Reflesiva. § Antisimétrica. § Transitiva.
|
Se llama clase de equivalencia [a] al conjunto de elementos que se relaciona con «a».
| · Clases de orden · Relación de orden total · Relación de orden parcial · Relación de orden lineal · Relación de orden estricto
|
Significado
Una relación binaria es una relación de equivalencia si y solo si es reflexiva, simétrica y transitiva. En otras palabras, si R es una relación de equivalencia, debe cumplir las siguientes propiedades: · Es reflexiva: ∀x ∈ A,(x,x) ∈ R ∀ x ∈ A, ( x, x) ∈ R. · Es simétrica: (x,y) ∈ R → (y,x) ∈ R ( x, y) ∈ R → ( y, x) ∈ R · Es transitiva: [(x,y) ∈ R ∧ (y,z) ∈ R] → (x,z) ∈ R [ ( x, y) ∈ R ∧ ( y, z) ∈ R] → ( x, z) ∈ R.
| Significado
es una relación binaria que pretende formalizar la idea intuitiva de ordenación de los elementos de un conjunto, es decir, que permite comparar sus elementos. Los conjuntos dotados de un orden, llamados conjuntos ordenados, son el objeto de estudio de la teoría del orden.
|
martes, 12 de septiembre de 2023
lunes, 4 de septiembre de 2023
-
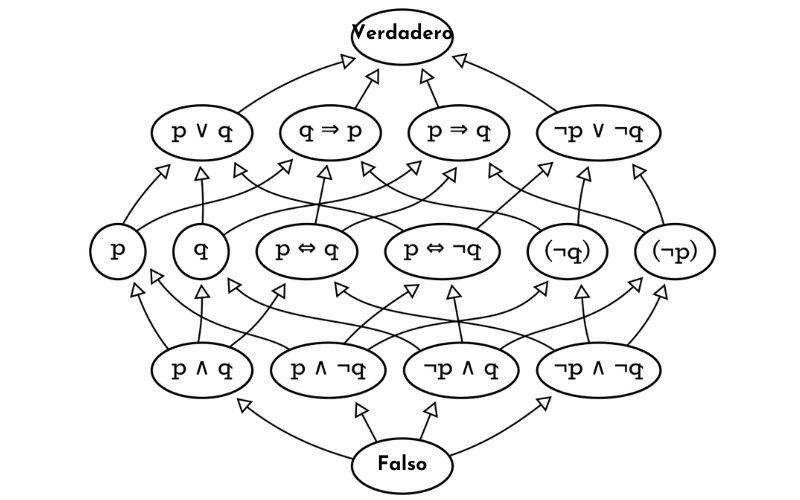
Álgebra booleana Diagrama de Hasse del álgebra booleana libre con dos generadores, p y q. Fuente: Chris-martin, Wikimedia Commons ¿Qué es ...
-
Procedimientos para convertir del sistema binario a octal El Sistema octal está compuesto por 8 números que van desde el 0 hasta el 7, d...












